< Coursera Ordered Data Structures >

Tree Terminology

• A tree is a linked structure with a sense of ancestry (parents, children, siblings, and more)!
• Each element in our tree is a node
• Each connection between two nodes is an edge
• Tree must always contain a root node that has no incoming edges.

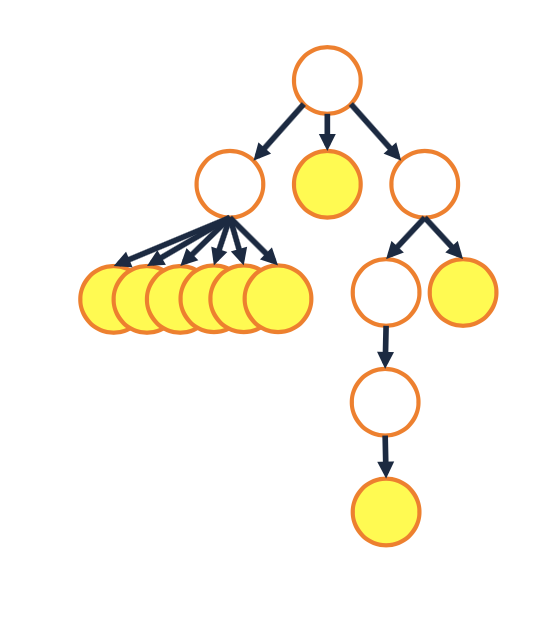
• Nodes that contain no outgoing edges are called leaf nodes.

• In a tree, the nodes will store data and amy be labeled.

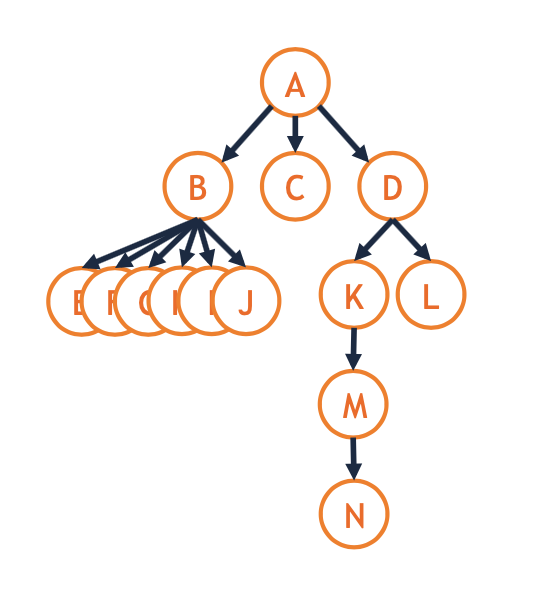
• Edges do not have names, but are referred to by the nodes they connect.

• Every node, except the root node, has exactly one parent node.

• A node’s children are the nodes with that node as it’s parent. (It’s possible to have anywhere from 0 to infinite children..)

• Most ancestry terms apply as expected:
  • Sibling : B and D are siblings
  • Ancestor : M, L, and D share A as a common ancestor
  • Grandchild / grandchildren : M is a D’s grandchild
  • Grandparent : D is M’s grandparent
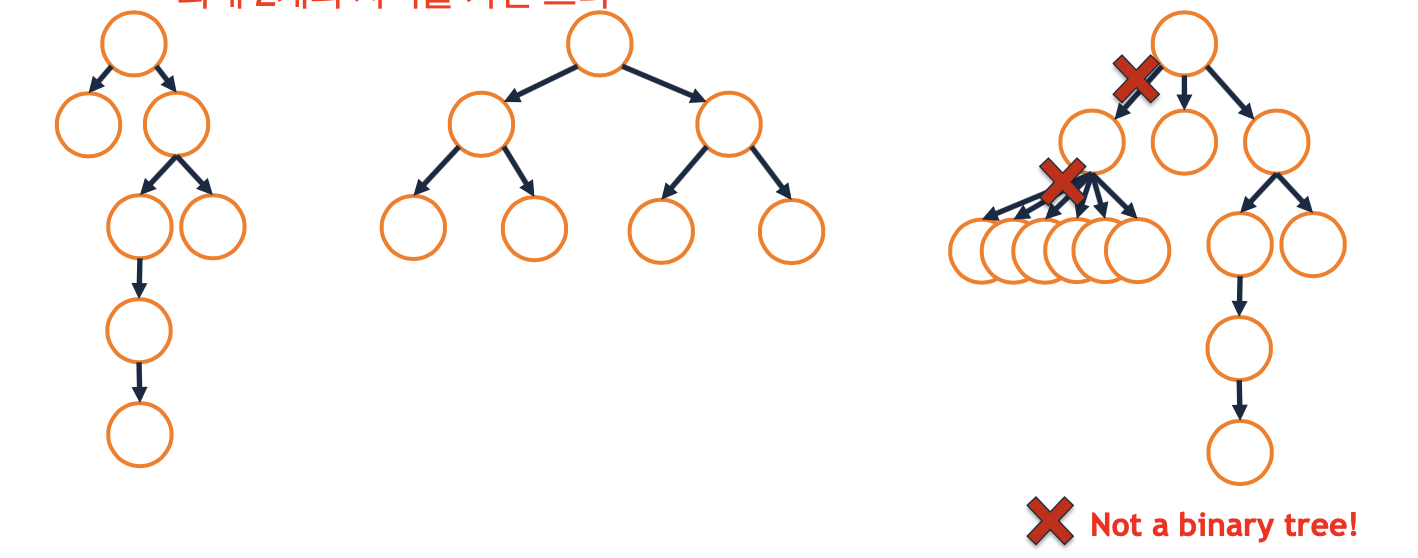
• Finally, to be a tree, tree conditions must be true:
  • Must have a root
  • Must have directed edges
  • Must not have a cycle (never have a loop)
  • => We say a tree is a “rooted, directed, and acyclic” structure.

Summary of Tree

• Trees formed with nodes and edges
• Trees must be rooted, directed, and acyclic
• The relationship between nodes in a tree follow classical ancestry terms (parent, child, etc)

Binary Trees

• A binary tree is a tree where every node has at most two children (maximum 2 children)

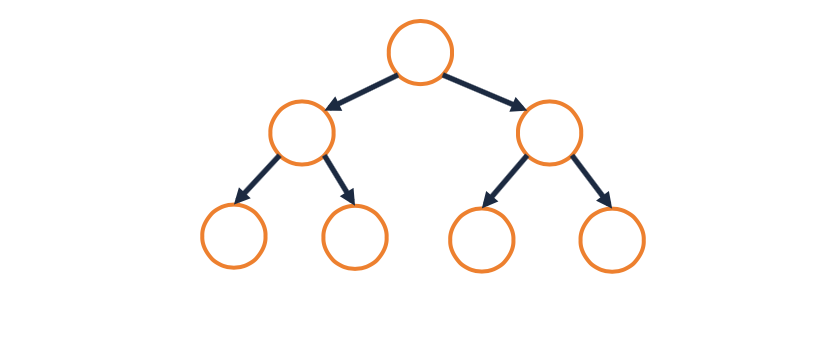
• In binary trees, we will label every child as either the “left child” or “right child” of its parent

#pragma once

template <typename T>
class BinaryTree {
  public:
    // ...

  private:
    class TreeNode {
      public:
        T & data;
        TreeNode* left;
        TreeNode* right;
        TreeNode(T & data) : data(data), left(nullptr), right(nullptr) { }
    };

    TreeNode *root_;
};

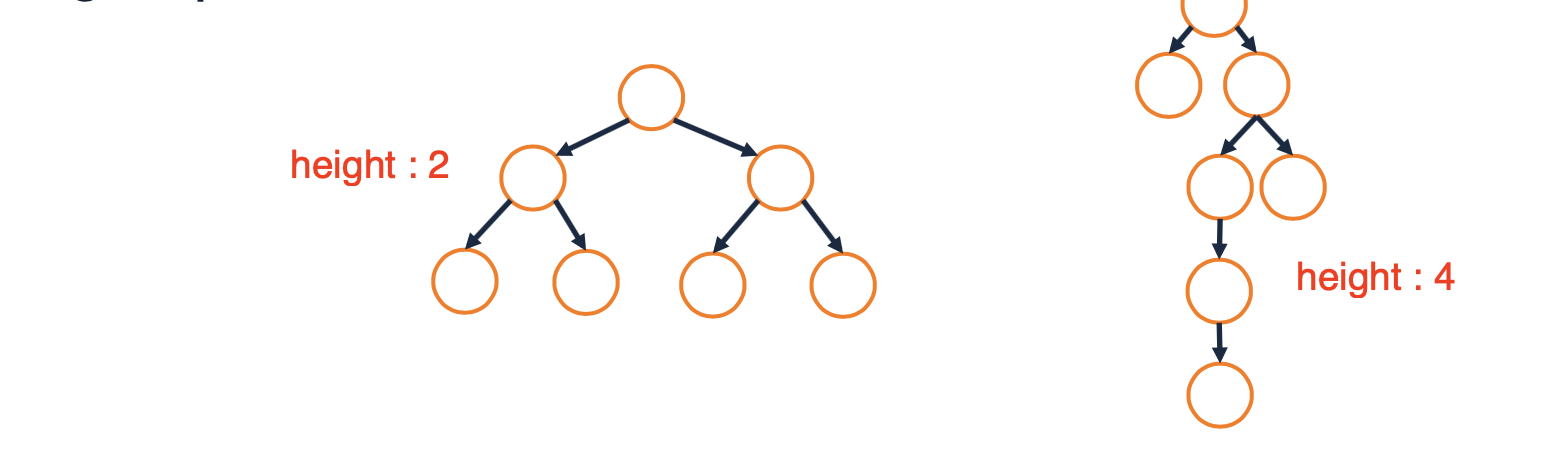
Binary Tree Property: Height

• The height of a binary tree is the number of edges in the longest path from the root to a leaf.

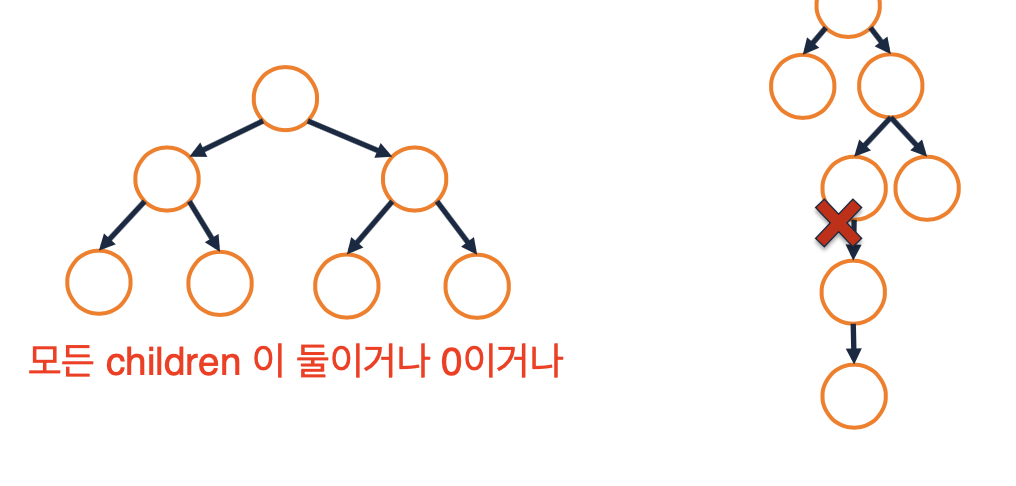
Binary Tree Property: Full

• A binary tree is full if and only if every node has either zero children or two children.

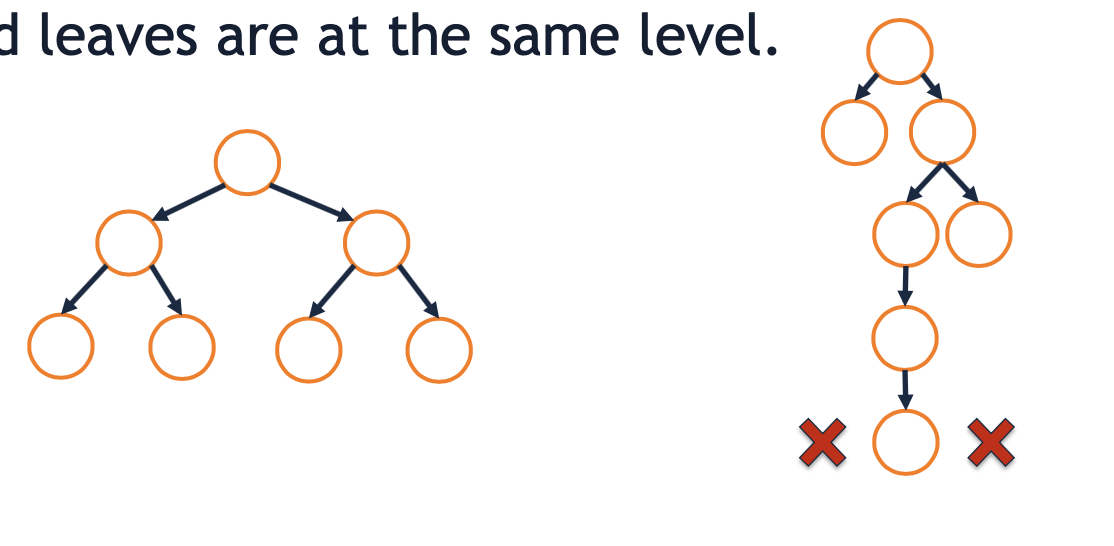
Binary Tree Property: Perfect

• A binary tree is perfect if and only if all interior nodes have two children and leaves are at the same level.

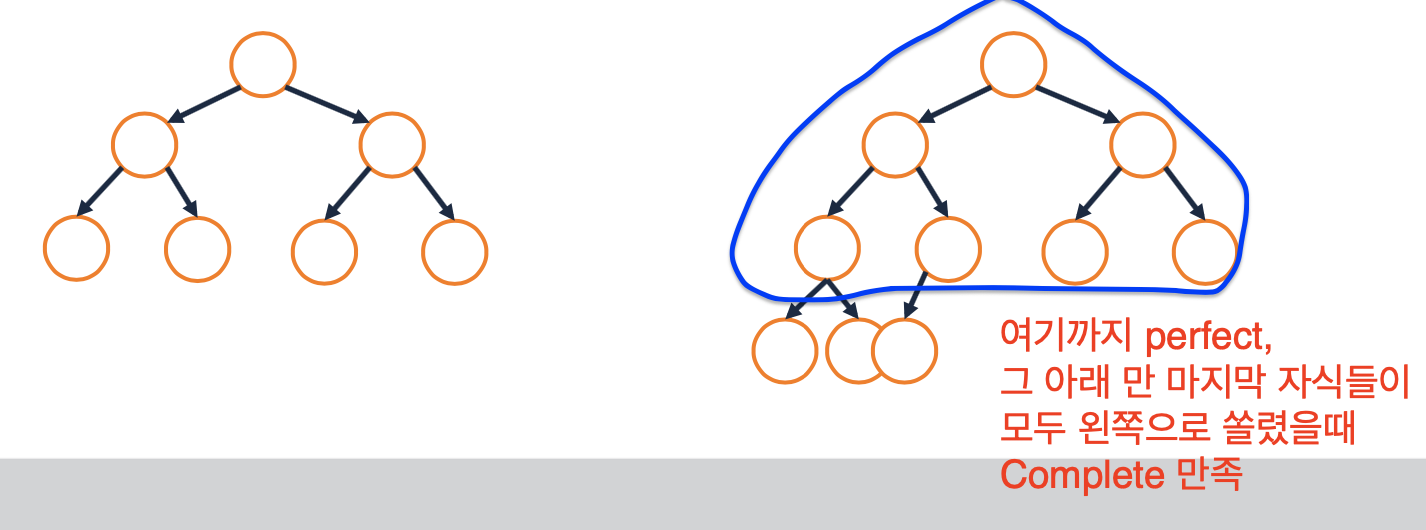
Binary Tree Property: Complete

• A binary tree is complete if and only if the tree is perfect up until the last level and all leaf nodes on the last level are pushed to the left.

Puzzle:

• Is a full tree complete?
  • NO.
  • full tree is the tree that has only one or two children
  • complete tree is the tree that is perfect and left biased
  • If a full tree’s last right-node has two children, it is not a complete tree because it’s right biased.
• Is a complete tree full?
  • NO.
  • If a complete tree’s last node is left biased but has only left node, it’s not a full tree.
  • 

Summary of Binary Trees

• Binary Trees are a special case of a tree where each node has at most two children.
• The children of binary trees are referred to as the “left child” and “right child”.

Tree Traversal

• One of the most important aspects of trees is how do we get the data out of a tree. How do we visit every single node and in what order do we visit these nodes? All of these topics is covered on this idea of a tree traversal.

Pre-order Traversals

• Pre-order traversal : shout, go left node, go right node
• It’s called pre because that’s when we actually did the shouting out. That’s when we did the visit of the node.

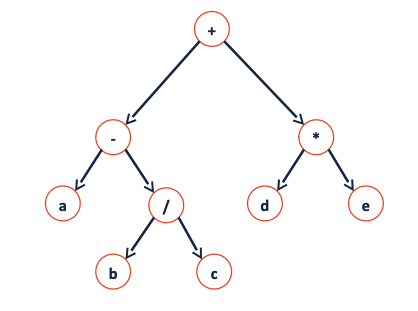
• Let’s pre-order traverse Shout(S) -> Left(L) -> Right(R) node

  1. + : S L R -> Shout, then go left node
  2. - : S L R -> Shout, then go left node
  3. a : S L R -> Shout, there’s no left neigther right node, so we’re done with this node. Go to the right node of -
  4. / : S L R -> Shout, then go left node
  5. b : S L R -> Shout, there’s no left neigther right node, so we’re done with this node. Go to the right node of /
  6. c : -> Shout, there’s no left neigther right node, so we’re done with this node. Go to /, we’re done with this nodje, go -, we’re done with this node …. Go to the right node of +
  7. * : -> Shout, then go left node
  8. d : -> Shout, there’s no left neigther right node, so we’re done with this node.Go to the right node of *
  9. e : Shout.

  => We shouted + - a / b c * d e , every single nodes of the tree.

• If we think about the source code for this, that simply means we need to print out the value of our node. Then after we print out the value of our node then we do a recursive call to the left child and the right child.

template<class T>
void BinaryTree<T>::preOrder(TreeNode * cur) {
  if(cur != NULL) {
  	shout(cur);
 	 	preOrder(cur->left);
  	preOrder(cur->right);  
  }
}

In-order traversal

• Left -> Shout -> Right

template<class T>
void BinaryTree<T>::inOrder(TreeNode * cur) {
  if(cur != NULL) {
 	 	preOrder(cur->left);
    shout(cur)
  	preOrder(cur->right);  
  }
}

• Let’s in-order traverse (L S R)

  1. + : L S R -> go to the left node
  2. - -> go to the left node
  3. a -> there’s no left node, so shout it out.
  4. There’s no right node, so go back to - and shout it out.
  5. Go to the right node of - which is /
  6. Go to the left node of / which is b, and since there’s no left node, shout b
  7. Since there’s no right node, go back to / and shout /.
  8. Go to the right node of / which is c, and since there’s no left node, shout c
  9. Since there’s no right node of c, go back until + and shout +
  10. Go to the right node of + which is * and go to the left node of * which is d
  11. SInce there’s no left node of d, shoud d
  12. Since there’s no right node of d, go to * and shout *
  13. Go to the right node of * which is e, and since there’s no left node of e, shout e
  14. Since there’s no right node of e the traversal ends here.

  => We shouted a - b / c + d * e

• So this tree happens to be a algebraic tree where we have a math equation encoded in the tree. If we add parentheses for layers then we can see that this code exactly shows us how we might go about encoding a math equation into a tree.

Post-order traversal

• Left -> Right -> Shout

template<class T>
void BinaryTree<T>::postOrder(TreeNode * cur) {
  if(cur != NULL) {
 	 	preOrder(cur->left);
  	preOrder(cur->right);  
    shout(cur)
  }
}

• Let’s post-order traversal (L R S)

  1. start from +, go to the left node which is -
  2. go to the right node of - which is a
  3. since there’s no left and right node, shout a
  4. go back to - and go to the right node of - which is /
  5. go to the left node of / which is b
  6. since there’s no left and right node, shout b
  7. go to the right node of / which is c
  8. since there’s no left and right node, shout c
  9. go back to / and since we already visited left and right node, shout /
  10. go back to - and since we already visited left and right node, shout -
  11. go back to + and go to the right node of + which is *
  12. go to the left node of * which is d
  13. since there’s no left and right node, shout d
  14. go to the right node of * which is e and shout e since there’s no left and right node
  15. go back to * and shout * since we already visited left and right node
  16. go back to + and shout + since we already visited left and right node

  => We shouted a b c / - d e * +

• So what you saw is we didn’t vary the tree at all through this entire process. Instead, the only thing we did was change when we shouted out the node. Either at the beginning, before left and right, in the middle in an inorder or at the end, in a postorder.

Level-order traversal

• A level order traversal is going to read every single level, one level at a time. You’re going to read the plus, the first level. Then the second level, then the third level, left to right.

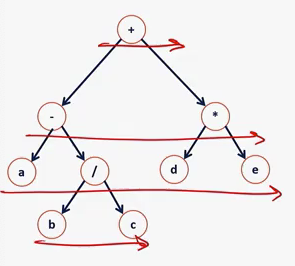
• Let’s level-order traverse.

  1. first-level : +
  2. second-level : - *
  3. third-level : a / d e
  4. Fourth-level : b c

  => We visited + - * a / d e b c

Traversal VS Search

• Traversal:

  Doing a traversal requires that every single node is visited

• Search:

  A search allows us to discover a particular node throughout the tree.

=> So when we discover a node in the tree, we may not visit every single node. We may use a strategy developed into traversal to help us find a node quickly but a search ends as soon as we find that node while a traversal is going to visit up to every single node.