< Coursera Ordered Data Structures >
Queue
- A queue is a first-in first-out data structure that is similar to waiting in a line or “queue”:
Abstract Data Type
In data structures, we will always begin our analysis asking “how can this structure be used with data?”
- A structure’s Abstract Data Type (ADT) is how data interacts with the structure.
- An ADT is not an implementation, it is a description
Queue ADT
- create : creates an empty queue
- push : adds data to the back of the queue
- pop : removes data from the front of the queue
- empty : returns true if the queue is empty
Example:
Consider four operations:
- Create a queue of integers.
- Push the number 4 to the queue.
- Push the number 2 to the queue.
- Pop a number from the queue.
#include <iostream>
#include <queue>
int main() {
// Create a std::queue:
std::queue<std::string> q;
// Add several strings to the queue:
q.push( "Orange" );
q.push( "Blue" );
q.push( "Illinois" );
// Print the front of the queue out and pop it off:
std::cout << "First pop(): " << q.front() << std::endl;
q.pop();
// Add another string and then print ouf the front of the queue:
q.push( "Illini" );
std::cout << "Second pop(): " << q.front() << std::endl;
return 0;
}
output
First pop(): Orange
Second pop(): Blue
Implementation
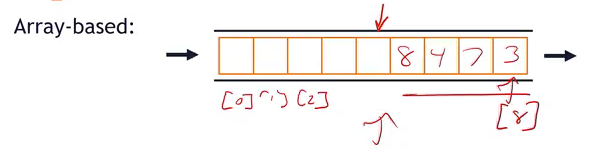
Array-based
-
In an array-based queue, an array’s going to sit in the queue and will have an index for each element in the array.
- We can expand the size by doubling the size, shirinking it by half the size as we need to.
- When the element arrives we simply add it to the queue.
- The element newly arrives is placed further back in the queue.
- In this array-based queue, notice that we can always have a counter to this term in the index where we should enter things next. We can always keep track of the index.
- There’s a number of different ways to set up the arrays, but so long as you keep track of where the insertion point is and where the removal point is or where the pop and push points are, we can always just adjust them by adding one or subtracting one and resizing the array as needed.
- All of these operations are just operation of indices and are always going to run in O of one time.
O(1)
List-based

- tail pointer : a pointer that accesses the last element of list
- When we put the new element at the back of the list-based queue, we only need to change the pointer of new element to the last element. =>
O(1) - If we want to add a new element at the head of the queue, we only need to change the pointer of the head_ =>
O(1)
Comparison
Objective: Create a Queue Data Structure
| Array | Linked List | |
|---|---|---|
| Create | O(1) | O(1) |
| Push | O(1)* Amortized runtime; occasional need to double the capacity of the array. |
O(1) |
| Pop | O(1)* Amortized runtime; occasional need to shrink the size of the array to free unused memory. |
O(1) |
| Empty | O(1) | O(1) |
- By using queue, a constant amount of operation time(O(1)) is guaranteed.
Queue Summary
- A queue is a first-in first-out data structure that is similar to waiting in a line.
- A queue may be implemented with an array or a doubly-linked list.
- Both an array-based and a list-based implementation can be built to run in constant, O(1) running time.
Stack
- A stack is a last-in first-out data structure that is similar to pile (“stack”) of papers.
Stack ADT
- create : creates an empty stack
- push : adds data to the top of the stack
- pop : removes data from the top of the stack
- empty : returns true if the stack is empty
#include <iostream>
#include <stack>
int main() {
// Create a std::stack:
std::stack<std::string> s;
// Add several strings to the stack:
s.push( "Orange" );
s.push( "Blue" );
s.push( "Illinois" );
// Print the front of the stack out and pop it off:
std::cout << "First pop(): " << s.top() << std::endl;
s.pop();
// Add another string and then print ouf the front of the stack:
s.push( "Illini" );
std::cout << "Second pop(): " << s.top() << std::endl;
return 0;
}
output
First pop(): Illinois
Second pop(): Illini
Comparison
| Array | Linked List | |
|---|---|---|
| Create | O(1) | O(1) |
| Push | O(1)* Amortized runtime; occasional need to double the capacity of the array. |
O(1) |
| Pop | O(1)* Amortized runtime; occasional need to shrink the size of the array to free unused memory. |
O(1) |
| Empty | O(1) | O(1) |
Summary of Stack
- A stack is a las-in first-out (LIFO) data structure that is similar to a pile (“stack”) of papers.
- A stack may be implemented with an array of a linked list.
- Both an array-based and a list-based implementation can be built to run in constant, O(1) running time.