< Coursera Ordered Data Structures >
Arrays
- An array stores data in blocks of sequential memory

#include <iostream>
int main() {
// Create a fixed-sized array of 10 primes:
int values[10] = {2, 3, 5, 7, 11, 13, 15, 17, 21, 23};
// Outputs the 4th (index 3) prime:
std::cout << values[3] << std:endl;
return 0;
}
- Similar to Java, in C++, put the variable with data structure(int) and the size of array(10) and store the data with {}
Array Limitation #1
-
All data in an array must be of the same type
-
two facts about arrays:
- Elements are all the same type
- The size (number of bytes) of the type of data is known
We can calculate the offset to any given index from the start of the array

-
What is the offset to index 3?
sizeof(Cube): 8 bytes- Then, the offset to index 3 from the beginning of the array(index 0) should be 3 * 8 bytes = 24 bytes
#include <iostream>
int main() {
// Create a fixed-sized array of 10 primes:
int values[10] = {2, 3, 5, 7, 11, 13, 15, 17, 21, 23};
// print the size of each type `int`:
std::cout << sizeof(int) << std::endl;
// => 4 (int is 4bytes)
// Using pointer arithmetic, ask the computer to calculate
// the offset from the beginning of the array to [2]:
int offset = (long)&(values[2]) - (long)&(values[0]);
std::cout << offset << std::endl;
// => 8 (difference of the size between two values are 8 bytes)
return 0;
}
- What does
offsetmean here?- difference of the address(or size) of two values
(long)&(values[2]): 140732910159192(long)&(values[0]): 140732910159184- => offset : 8 (because
values[2]is located two indices after thanvalues[0])
#include <iostream>
int main() {
// Create an array of 3 `Cube`s:
Cube cubes[3] = { Cube(11), Cube(42), Cube(400)};
// Print the size of each type `Cube`:
std::cout << sizeof(Cube) << std::endl;
// => 8 bytes
// Using pointer arithmetic, ask the computer to calculate
// the offset from the beginning of the array to [2]:
int offset = (long)&(cubes[2]) - (long)&(cubes[0]);
std::cout << offset << std::endl;
// => 16
return 0;
}
- Cube has 8 bytes each
- So, the variable offset should be 16 bytes.
Array Limitation #2
- Arrays have a fixed capacity.
- Arrays must store their data sequentially in memory.
- The capacity of an array is the maximum number of elements that can be stored.
- The size of an array is the current number of elements stored in the array.
- An array is full when the size of the array is equal to the capacity
- The only way to add another element : to allocate a new, larger array and copy over all of the data
std::vector
-
The
std::vectorimplements an array that dynamically grows in size automatically. However, all properties remain true:- Array elements are a fixed data type.
- At any given point, the array has a fixed capacity.
- The array must be expanded when the capacity is reached.
#include <iostream>
#include <vector>
#include "../Cube.h"
using uiuc::Cube;
int main() {
std::vector<Cube> cubes{ Cube(11), Cube(42), Cube(400) };
// Examine capacity:
std::cout << "Initial Capacity: " << cubes.capacity() << std::endl;
cubes.push_back( Cube(800) );
std::cout << "Size after adding: " << cubes.size() << std::endl;
std::cout << "Capacity after adding: " << cubes.capacity() << std::endl;
// Using pointer arithmetic, ask the computer to calculate
// the offset from the beginning of the array to [2]:
int offset = (long)&(cubes[2]) - (long)&(cubes[0]);
std::cout << "Memory separation: " << offset << std::endl;
// Find a specific `target` cube in the array:
Cube target = Cube(400);
for (unsigned i = 0; i < cubes.size(); i++) {
if (target == cubes[i]) {
std::cout << "Found target at [" << i << "]" << std::endl;
}
}
return 0;
}
Output
Initial Capacity: 3
Size after adding: 4
Capacity after adding: 6
Memory separation: 16
Found target at [2]
- After add one more element that takes over the initial capacity (3),
vectorautomatically double the capacity (6) - Memory separation :
cubes[2]is two cubes aftercubes[0]=> 2 * 8bytes = 16 bytes
Linked Memory

-
Linked memory stores data together with a “link” to the location (in memory) of the next list node
-
A ` list node` refers to pair of both the data and the link
-
// C++ ListNode Class: template <typename T> class ListNode { public: // Member variable T & data; // since we don't know the data type, we use generic form of 'T' ListNode *next; // refers to the next listnode that is linked with the previous one // constructor ListNode(T & data) : data(data), next(NULL) {} // stores data and next }
-
-
Zero or more
ListNodeelements linked together to form a Linked List- A pointer called the “head pointer” stores the link to the beginning of the list
- A pointer to NULL marks the end of the list
#pragma once
template <typename T>
class List {
public:
// member functions
const T & operator[](unsigned index);
void insertAtFront(const T & data);
private:
class ListNode {
public:
const T & data;
ListNode *next;
ListNode(const T & data) : data(data), next(nullptr) { }
};
ListNode *head_; /*< Head pointer for our List */
ListNode* _find(const T & data);
};
// Finish including the rest of the header from the additional header file.
// This is just done to spread out our writing among more manageable files.
#include "List.hpp"
-
What is
operator[]?- We can access the list l.
- Forexample
List <int> l,l[0]is going to calloperator[](unsigned index)function. - It defines what CPP should do when we call the operator
[].
List::get
- Objective : Return the element at index k.
template <typename T>
const T & List<T>::operator[](unsigned index) {
// Start a `thru` pointer to advance thru the list:
ListNode *thru = head_;
// Loop until the end of the list (or until a `nullptr`):
while (index > 0 && thru->next != nullptr) {
thru = thru->next;
index--;
}
// Return the data:
return thru->data;
}
- What does the
while loopdo here?- forexample, we command
l.get(4) thrustarts froml[0]indexis 4- in the loop,
thrubecomesl[1]andindexbecomes 3thrubecomesl[2]andindexbecomes 2thrubecomesl[3]andindexbecomes 1thrubecomesl[4]andindexbecomes 0- since
indexis not bigger than 0 anymore, the loop stops
- and return the data that
thrurefers to, which isl[4].
- forexample, we command
List Runtime
- In a list, the time it takes to access a given index grows based on the size of the list
- In contrast, an array can access any element in a constant, fixed amount of time. Therefore, for accessing a given index, an array is faster than a list.
- For example, if we want to access
l[10000], we should go through 10000 times of listnodes to find it.
List::insert
- Objective: Add an element to the list
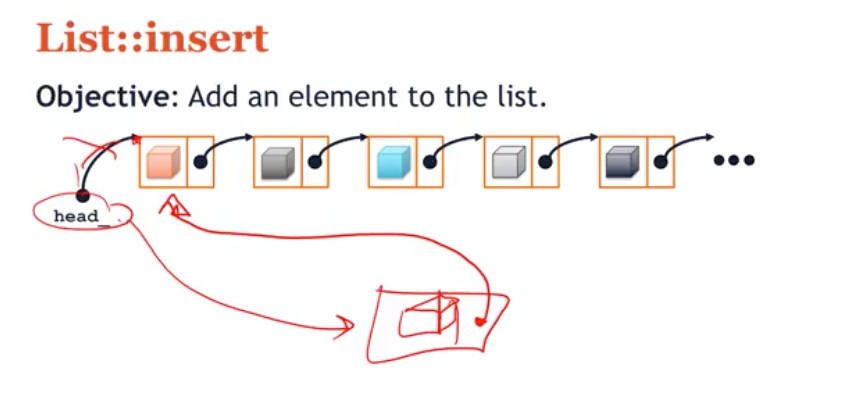
- To insert a new cube in the list, I simply need to make
head_points to my new cube, and the pointer of the new cube points the previous first cube. In this way, I don’t even need to look at the rest of the list!
template <typename T>
void List<T>::insertAtFront(const T & data) {
// Create a new ListNode on the heap:
ListNode *node = new ListNode(data);
// Set the new node’s next pointer point the current
// head of the List:
node->next = head_;
// Set the List’s head pointer to be the new node:
head_ = node;
}
List Capacity
- In a list, the capacity is bounded only by the memory available on the system. We can just add new elements again and again to the list.
- In contrast, an array has a fixed capacity. A list is a more flexible data structure than an array.
Data Types
- In both arrays and lists, all data within an instance of a container must be the same type.
- An integer {array, list} must only contain integers.
- A String {array, list} must only contain strings.
int main() {
List<int> list;
std::cout << "Inserting element 3 at front..." << std::endl;
list.insertAtFront(3);
std::cout << "list[0]: " << list[0] << std::endl;
std::cout << "Inserting element 30 at front..." << std::endl;
list.insertAtFront(30);
std::cout << "list[0]: " << list[0] << std::endl;
std::cout << "list[1]: " << list[1] << std::endl;
return 0;
}
output
Inserting element 3 at front...
list[0]: 3
Inserting element 30 at front...
list[0]: 30
list[1]: 3
Linked Memory (Summary)
- Linked memory stores data in “nodes” linked together by “links” (pointers).
- A basic linked memory structure is a Linked List, which consists of zero or more
ListNodeslined together and a head pointer. - A linked list provides a flexible alternative to an array.
Runtime Analysis
- It is important to know how the runtime is different by data structure.
-
Run-time Analysis allows us to formalize a method of comparing the speed of an algorithm as the size of input grows.
-
Run-time Analysis allows us to formalize a method of comparing the speed of an algorithm as the size of input grows.
-
We summarize the runtime in “Big-O notation”, leaving only the term that dominates the growth:
O(1), constant timeO(n), linear timeO(n^2), polynomial time (다항의)
Access a Given Index
- Array :
O(1)- Direct access via offset formula (using [] operation) - List :
O(n)- Must traverse every element to reach the index
Insert at front
(insert an element at the front)
- Array :
O(1)*- Amortized constant time when array size is doubled when copied - List :
O(1)- Fixed constant time by adding the new data at the head of the list
cf) Amortized : to spend the constant time time by time
Find Data
(Given data, find the location of that data in the collection)
- Array:
- I have no choice but start from first element and keep going until find the right data
- The time spent to find the right data would be equal to the amount of the data in the collection
O(n)
- List:
- Start from
head_and travel through every single element until find the right data O(n)
- Start from
Find Data in a Sorted Array
(Given data, find the location of that data in the collection)
-
Array:
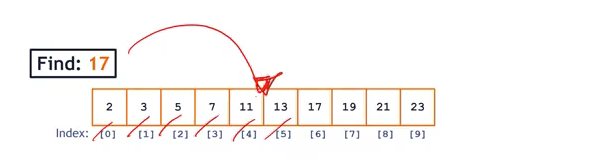
- Why don’t we start from the middle of the array if it’s sorted?
- We know that 17 is on the right side of 13.
- Next, we know that 17 is on the left side of 19.
- => This is called Binary Search. We cut it in half each time, and that’s
O(lg~2(n))operation.
-
List:
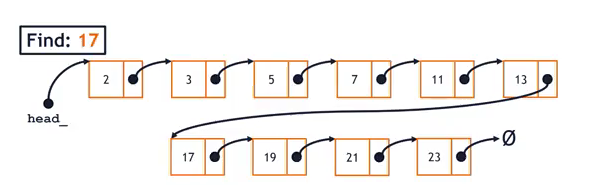
- We can’t jump to the middle of the list!
- The best we can to is still travel the whole ListNodes!
- => even if the data is sorted, it’s still
O(n)
Insert After
(Given an element (ListNode or index), insert a new element immediately afterwards)
-
Array:
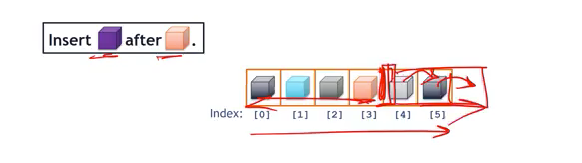
- We have to copy the data that is already after the orange cube, move all data over, and once it’s moved, we have room to insert the purple cube.
- We need to move n/2 elements ->
O(n)of total moves.
-
List:
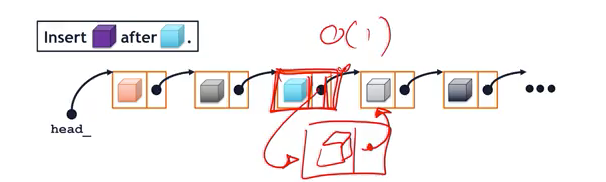
- We can just create new ListNode, put the blue one, and change the pointers!
- =>
O(1)
Delete After
(Given an element (ListNode or Index), delete the element immediately afterwards)
- Array:
O(n)(same logic as insert after) - List:
O(1)(same logic as insert after)
Array and List Operations
- Arrays and Lists are both ordered collections that have complex tradeoffs between run-time and flexibility.
- We will build data structures using these primitive structures.